Creating natural paths on terrains using pathfinding
Pathfinding is not just for finding paths for AI agents/NPCs and similar. It’s also for procedurally creating paths.

While working on path creation for a procedural terrain, I had the problem that the generated paths would keep having too steep sections, like this:

It was too steep and also didn’t look natural at all. I kept increasing the cost multiplier for slopes, but it didn’t help.

Then it hit me: My function just penalized the vertical distance, but it didn’t make any difference if this vertical distance came gradually or all at once.
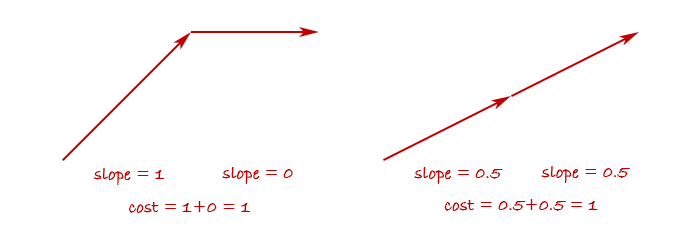
So in fact, my cost function wasn’t trying to avoid steepness - rather it was trying to make a path where the altitude changes monotonically. It would do everything it could to avoid the path first going up and then down again.
But I didn’t care if the path went a little up and down, as long as it wasn’t too steep at any point. To achieve this behavior, I needed to penalize steep slopes more than linearly, for example by squaring it.

This has the effect of penalizing abrupt changes in altitude and reward gradual changes.

And sure enough, after the change the generated paths avoided steepness and looked much more like what humans would create.

Tweaking pathfinding cost functions is one of those odd little things that I really enjoy. Seeing a little change in a formula imbue a generated creation with what could be mistaken for human design is really fascinating and fun!
Further notes
The observation-turned-blog-post in its original form ended there, but I've compiled some further notes for those who want to dig into the details.
Pathfinding method
Let me tell about the method I use for the pathfinding, since I was asked about this. I won't do an introduction to pathfinding in general here but assume understanding of the principles of performing pathfinding using an algorithm like A* or similar on a graph of nodes connected by edges.
Such a graph can be represented in many ways. Sometimes it's a data structure with explicit data representing all the nodes and edges and how they're connected. Other times it can just be a grid (like a 2D array) and each cell is implicitly connected to the neighboring cells - maybe the 4 or 8 neighbors, depending on whether diagonal connections are used.
It doesn't really matter, and a pathfinding algorithm can typically easily be modified to work with one or the other. Apart from giving it a start node and goal node, the important part is that you can tell the algorithm:
- Which other nodes are a node connected to?
- What is the real or estimated cost of getting from one node to another?
You might have data for this stored in advance or you might calculate the answers on the fly when asked.
For the terrain pathfinding I do the latter. In fact, there is neither an explicit graph, nor any 2D array. There is no data structure at all for the pathfinding to happen inside. Instead, it's all implicit, based solely on coordinates. I tell the pathfinder what the start and end coordinates are, and there's a function for getting "neighbor coordinates" to a given coordinate. There's also a function for getting the cost of getting from one coordinate to another, as you saw earlier.
This may sound completely free-form and magical at first, but there still is a structure that must be adhered to. You must imagine a grid structure and ensure the coordinates always fall within this grid. In my case it's a plain quadratic cell grid where each cell has a size of 5. So the start coordinate, goal coordinate, and every provided neighbor coordinate must always have x and y values that are multiples of 5. You also shouldn't use floating-point numbers for this, since they can produce floating point precision errors, and even the slightest imprecision can cause the pathfinding to completely fail.
I wanted my paths to be able to have a natural, non-jagged look, so I wanted edges to come in 16 directions instead of the basic 8. The 8 additional directions are achieved by going two cells out and one to the side. This provided me with an interesting choice of whether the 8 other directions should also go two cells out, or just one.

In theory the second option can be weird, since if you need to move just one cell the path have to first side-step by two cells. But in practice both seems to work fine. The first images in this post were made with the first option but I later decided to use the second to avoid the path having very small-scale zig-zags.
Effects of different parameter values
I got asked on the proceduralgeneration sub-reddit:
How rapidly does the path change as you increase the power from 1.0 to 2.0? What happens if you go past 2.0? Does the path eventually have to spiral around the mountain or something?
I had actually been content just using the values I had found which seemed to work well enough, but now that I'd been asked, of course I wanted to find the answers too! I tried doing the pathfinding with the power values 1.5, 2.0 and 3.0 and with the multiplier values 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, and 25. I had moved the multiplier inside the power function since the original version of the code, so those multipliers are multiplied onto the steepness before the resulting value is raised to the given power. Here's a table of the results.

Some notes on the result.
Overall the common theme is that the results range from straight and boring to wildly tortuous. At the extreme end, the path begins to create loops - something that should be impossible with path-finding. However, the edges I use in the path-finding can cross each other. This means that they can appear to loop even though they never pass through the same points from the perspective of the path-finding. They only begin to do this once the path-finding is so extremely sensitive to tiny changes in altitude that the small difference in altitude between one of two crossing edges is enough for it to exploit it to loop around. I should say that I only sample the altitude at the end-points of each edge, which appears to be fully sufficient except in the extreme cases like this.
Note that there are very similar occurrences across the different power values. For example, multiplier 10 at power 1.5 looks just like multiplier 6 at power 3.0, and multiplier 7 at power 2.0 looks just like multiplier 5 at power 3.0. Does this mean that any result you can get with one power value, you can also get with another? That there exists a transformation that means they're mathematically equivalent? No, I don't believe so. It feels like there's subtle differences. For example, the progression of paths with power value 3 begins to do loops before it begins to take a major detour, while for power value 2, the loops only start happening after it has begun doing a large detour. The differences are very subtle though and hard to put the finger on exactly.
One thing that's tempting to look for is qualitative differences, such as some paths doing many small zig-zags and others doing larger swoops. However, I think that's a red herring. The algorithms doesn't measure sharpness of turns or frequency of turns in any way and shouldn't be able to tell one from the other. I think that the seeming qualitative differences are thus up to unpredictable aspects of how the path-finding interacts with the terrain height function that sometimes just happen to produce one result or the other. To answer it in terms of the original question: If the terrain was perfectly conical, a path from the base to the top might equally well form a spiral, a zig-zag pattern, or any other combination of left-winding and right-winding sections.
My own pragmatic takeaway from this is that sticking with just a power value of 2 seems fine and I'd then use multiplier values between 3 and 15 depending on how straight or tortuous I want the path to be.
Perspectives
These generated paths were a proof-of-concept for a new project I'm working on and I'm sure I'll learn more as I go along. For example, already I'm learning some things about approaches for flattening the terrain around the paths which I may share at a later point when I'm a bit more sure of my findings. For now, I hope you found this useful!
2024 update: Code available
I've now released a framework called LayerProcGen as open source, and one of the sample scenes generates natural paths using the technique described in this article. So a fully functional implementation is now available for study and use.
11 comments:
Very interesting. What method do you use to flatten the terrain were your path flows?
@Lasse For these images I used a simple technique where for every point on the terrain, I find the closest point on the path, and depending on the distance to that point, interpolate between the initial terrain height and the height of that point. This works OK as you can see, but has some unfortunate artefacts in certain cases when looking closer. I've been experimenting with other approaches with some success but not ready to share that just yet.
Thanks, that makes sense :)
Interesting. Maybe you could share some code of your implementation. Would be really helpful
A complete research paper was published some years ago on that topic, you can check for instance the following document:
https://scholar.google.fr/citations?view_op=view_citation&hl=fr&user=yLkaxt8AAAAJ&citation_for_view=yLkaxt8AAAAJ:u-x6o8ySG0sC
Improvements were also published in the same international CG conference a year later.
Im trying to implement a similar path generating system in a project, yet i keep getting this error where previously visited coordinates are revisited and so it loops for a while before akwardly breaking out of the loop and continuing (i dont even know how this might be possible).
My question is, do you use any loop detecting mechanism?
I tried storing every assessed coordinate on a hashset and checking whether it is already contained in the set before assessing it.
It didnt work...
@Gabriel Mosz Pathfinding algorithms generally keep track of already visited nodes. How to fix it for your implementation depends on the details of your implementation, so I'm afraid I can't help with that.
I just released a framework called LayerProcGen and one of the sample scenes is generating terrain with paths using pathfinding based on the technique described in this article. So you can check out the implementation there for reference.
Framework:
https://github.com/runevision/LayerProcGen
Pathfinding code in terrain sample:
https://github.com/runevision/LayerProcGen/blob/main/Samples/TerrainSample/Scripts/Generation/TerrainObjects/TerrainPathFinder.cs
Thank you for creating this article and posting your code to GitHub. I have just started reading your documentation about top-down planning versus functional approaches to proc. gen., very interesting.
I am wondering if there are any good resources you can recommend for understanding the basic and most general concepts of the planning approach (especially in the context of an infinite world), as the functional approach is the only one I am familiar with at this time.
Also, have you made any articles about how you generate your heightmaps...they are simply wonderful!
@metapfhor I don't think there are a lot of resources about the planning approach specifically in the context of an infinite world. Like I write in the documentation, I'm not aware of any games that do this.
By releasing the LayerProcGen framework I'm hoping to further this approach to procedural generation, but it's something that the procedural generation community will have to explore and advance together.
For now I'd suggest to look at resources for top-down procedural planning for finite worlds and think about how it could be adapted to a chunk-based approach.
About my heightmaps, I wrote a bit about it here:
https://www.reddit.com/r/proceduralgeneration/comments/1900773/comment/krfxewo/
There is also a terrain demo included with LayerProcGen. The heightmap function there is a bit different, but you could check it out and see if you think that looks nice, or might be a good starting point for further tweaking.
Thanks for the links, I've been digesting your terrain demo (the blurb in the reddit post is a nice primer for ideas).
A bit lost as to what I should be reading for top-down procedural planning. Do you mean top-down perspective or like the approach starts from a top level and moves downwards? Feeling lost...any specific links?
@metapfhor By top-down I mean processes that start from the top. Examples are level generation for rogue-likes, procedural city generation, or really any other "planning" world generation where an algorithm decides which things should be where, how things should be connected, and so on.
You don't need to search for "top down" specifically. The idea with layer-based generation is not that you should specifically use a top-down approach; it's more that many types of procedural generation happen to be top-down, and with the layer-based approach, those are not off-limits even though things are generated in chunks. So there is more freedom to pick whatever procedural algorithm is fitting for a given task, although it may take some pondering to figure out how to adapt it to the layer-based approach.
I would recommend to decide on what it is you want to make and search for procedural generation sources on that subject.
This discussion is getting a bit off-topic for the article about roads and blog comments is also blog the best discussion format. If you have a reddit account you could post your questions in the procedural generation subreddit (I see all posts there so would be sure to spot it):
https://www.reddit.com/r/proceduralgeneration/
Alternatively, if you have a GitHub account you could also post in the discussions of the repo:
https://github.com/runevision/LayerProcGen/discussions
I'm also on Twitter/X and Mastodon.
Post a Comment